2023. 10. 3. 22:09ㆍML
지도학습 알고리즘
분류, 회귀
회귀 - 임의의 어떤 숫자를 예측, 두 변수사이의 상관관계를 분석하는 방법
K-nearest neighbor : 예측하려는 샘플에 가장 가까운 샘플 K개를 선택, 이 샘플들의 클래스를 확인하여 다수 클래스를 새로운 샘플의 클래스로 예측.
KNeighborsRegressor
결정계수 R^2 = (타깃-예측)^2의 합 / (타깃-평균)^2의 합
타깃이 평균정도 예측 → 0에 가까워짐
예측이 타깃에 가까워지면 →1에 가까워짐
overfitting vs underfitting
훈련 세트점수 높은데 테스트에서 점수가 나쁨→overfitting
훈련 세트에만 잘 맞는 모델, 새로운 샘플에 대한 예측 만들 때 동작 안됨
훈련 세트, 테스트 세트 점수 모두 낮거나 훈련세트 점수 낮은데 테스트 높음→ underfitting
K-nearest neighbor 알고리즘 모델 복잡하게 만드는법 → K를 줄이는것
LinearRegression
선형회귀로 훈련세트 범위 밖의 샘플 예측가능
특성과 타깃 사이의 관계를 가장 잘 나타내는 선형방정식 찾기
특성이 하나면 직선방정식
선형 회귀가 찾은 특성과 타깃 사이의 관계는 선형 방정식의 계수 또는 가중치에 저장
가중치는 방정식의 기울기, 절편
다항 회귀는 다항식사용 비선형일수 있지만 선형회귀로 표현 가능
다중회귀
여러개의 특성을 사용한 선형회귀
특성이 2개면 평면을 학습 타깃 = a특성1 + b특성2 + 절편
기존의 특성을 사용해 새로운 특성을 뽑아내는 작업→ 특성공학
특성의 개수를 크게 늘리면 선형모델 강력해짐→ 과대적합
규제 regularization
모델이 overfitting 되지 않도록 만드는것
선형회귀 → 계수(기울기)의 크기를 작게만드는 것
규제 적용하기전 정규화는 필수일까욤?
계수 값의 크기가 많이 다르면 공정하게 제어가 안됨
선형 회귀 모델에 규제를 추가한 모델 Ridge and Lasso
Ridge - 계수를 제곱한 값을 기준으로 규제
Lasso - 계수의 절댓값 기준
두 알고리즘 모두 계수의 크기를 줄임 , Lasso 는 0 가능
규제의 양 조절 alpha 값이 크면 계수값을 더 줄임 → underfitting 유도
alpha 값이 작으면 계수가 덜줄음, 선형회귀 모델과 유사해짐→overfitting 가능성 큼
하이퍼파라미터 → alpha 등,, 사람이 알려줘야 하는 파라미터
Lasso 모델 훈련중 경고 - 최적의 계수를 찾기위해 반복적인 연산 수행, 지정한 반복횟수가 부족할때 나옴
LogisticRegression - 이름은 회귀지만 분류모델
시구모이드 함수 - 선형 방정식의 출력을 0과1사이로압축 이진분류를 위해 사용
파이썬 np.exp()
Ridge와 같이 계수의 제곱을 규제 L2 규제
규제 제어하는 변수 C
C는 작을수록 규제가 쎔. 기본값 1
소프트맥스 함수는 주로 다중 클래스 분류 문제에서 사용되는 함수입니다. 이 함수는 입력된 값을 각 클래스에 대한 확률로 변환하는 데 사용됩니다. 다중분류에서 여러 선형 방정식의 출력 결과를 정규화하여 합이 1이되도록 만듦
확률적 경사 하강법-





하이퍼 파라미터 튜닝
라이브러리가 제공하는 기본값을 그대로 사용, 매개변수 바꿔보면서 훈련, 교차검증
매개변수 두개 바꿔가면서 최적값찾기 →그리드서치


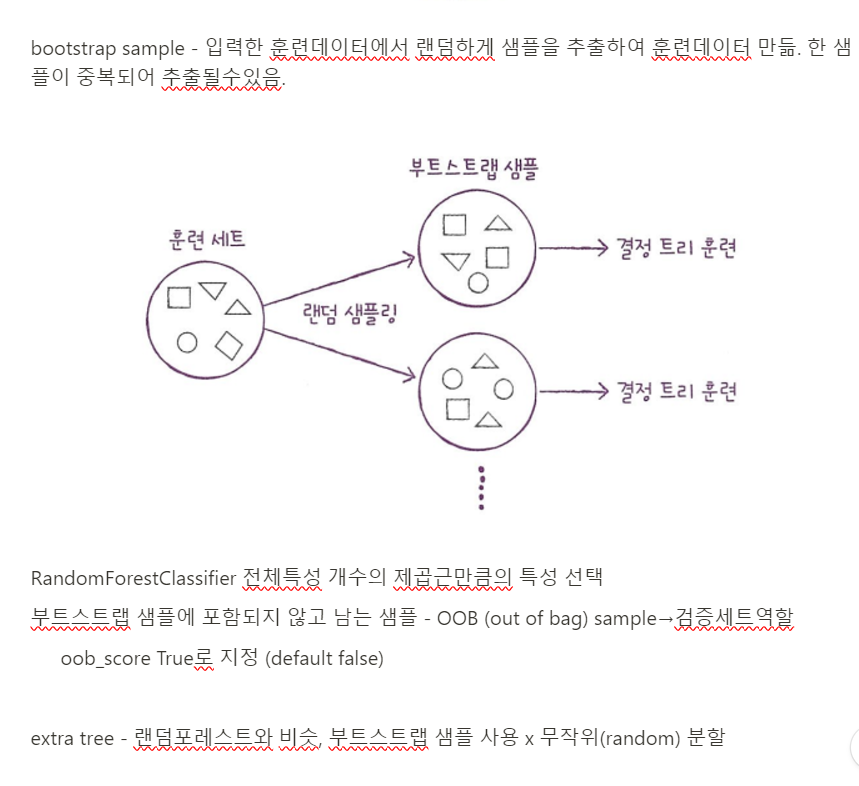
그레이디언트 부스팅 - 깊이가 얕은 결정 트리를 이용, 이전 트리의 오차를 보완하는 방식
트리 훈련에 사용할 훈련세트 비율 정하는 매개변수 subsample default 값 1.0 . 1.0보다 작으면 훈련세트 일부 사용, 랜덤 포레스트보다 조금 더 높은 성능, 순서대로 트리를 추가하기때문에 느림.
히스토그램 기반 그레디언트 부스팅 - 그레디언트 부스팅 속도와 성능 개선한 것
특성을 256개의 구간으로 나눔, 이 구간에서 하나를 떼어놓고 누락된 값을 위해서 사용
permutation_importance() → 특성을 하나씩 랜덤하게 섞어서 모델의 성능이 변화하는지를 관찰, 어떤 특성이 중요한지 계산, 훈련, 테스트세트에도 적용가능
unsupervised learning 비지도학습
타깃이 없을 때 사용
비슷한 샘플끼리 모으는것 clustrering 군집
군집 평균값 클러스터 중심, centroid
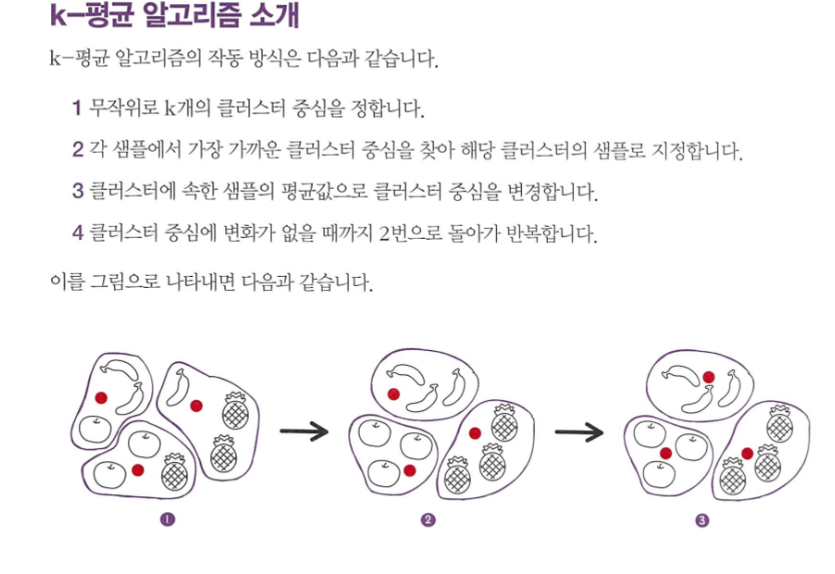
k-mean algorithm
최적의 K 찾기
엘보우 -클러스터 개수를 늘려가면서 이너셔의 변화를 관찰하여 최적의 클러스터 개수 찾는방법
k-mean algorithm을 통해 클러스터 중심과 클러스터에 속한 샘플사이의 거리 잴수있음. 이 거리의 제곱합을 이너셔라고함. 이너셔는 클러스터의 샘플이 얼마나 가까이 있는지를 나타냄.

차원 - one of 특성..?
차원을 줄여서 저장공간 줄임
2차원배열에서 차원 - 행,열
1차원배열 - 원소개수가 차원. 5개원소 있으면 5차원
Dimensionality reduction 차원축소 - 데이터를 가장 잘 나타내는 일부 특성 선택, 데이터 크기를 줄이고 지도학습모델의 성능 향상시키는방법
PCA (principal component analysis) 차원축소 알고리즘
데이터에 있는 분산이 큰 방향을 찾는것
벡터를 주성분으로 부름. 주성분 벡터의 원소개수는 원본 데이터셋에 있는 특성 개수와같음.
원본데이터는 주성분을 사용해 차원을 줄일 수 있음. 주성분에 직각으로 투영

주성분은 원본차원과 같고 주성분으로 바꾼 데이터는 차원이 줄어듦.
주성분에 투영하여 바꾼 데이터는 원본이 가지고 있는 특성을 가장 잘 나타내고있음.
첫번째 주성분을 찾은 다음 이 벡터에 수직이고 분산이 가장 큰 다음방향을 찾음. 이벡터가두번째 주성분 . 일반적으로 주성분은 원본 특성의 개수만큼 찾을 수 있음.
설명된 분산은 주성분이 원본 데이터의 분산을 얼마나 잘 나타내는지 기록한값
Reference)
혼자공부하는 머신러닝 딥러닝